carma_wm::geometry Namespace Reference

geometry namespace contains utility geometry functions which do not require the map or route provided by an active world model More...

Functions
TrackPos	trackPos (const lanelet::ConstLanelet &lanelet, const lanelet::BasicPoint2d &point)
	Returns the TrackPos, computed in 2d, of the provided point relative to the centerline of the provided lanelet. Positive crosstrack will be to the right. Points occuring before the segment will have negative downtrack. See the matchSegment function for a description of the edge cases associated with the max_crosstrack parameter. More...
TrackPos	trackPos (const lanelet::BasicPoint2d &p, const lanelet::BasicPoint2d &seg_start, const lanelet::BasicPoint2d &seg_end)
	Return the track position of a point relative to a line segment defined by two other points. Positive crosstrack will be to the right. Points occuring before the segment will have negative downtrack. More...
std::tuple< TrackPos, lanelet::BasicSegment2d >	matchSegment (const lanelet::BasicPoint2d &p, const lanelet::BasicLineString2d &line_string)
	Get the TrackPos of the provided point along the linestring and the segment of the line string which the provided point should be considered in. More...
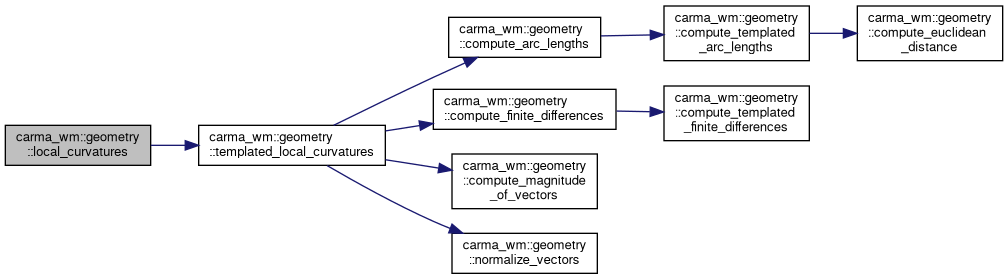
std::vector< double >	local_curvatures (const lanelet::BasicLineString2d &centerline_points)
	Returns a list of local (computed by discrete derivative) curvatures for the input centerlines. The list of returned curvatures matches 1-to-1 with with list of points in the input centerlines. More...
std::vector< double >	local_curvatures (const std::vector< lanelet::BasicPoint2d > &centerline_points)
std::vector< double >	local_curvatures (const std::vector< lanelet::ConstLanelet > &lanelets)
	Specialized overload of the centerline local_curvatures method but for lanelets. More...
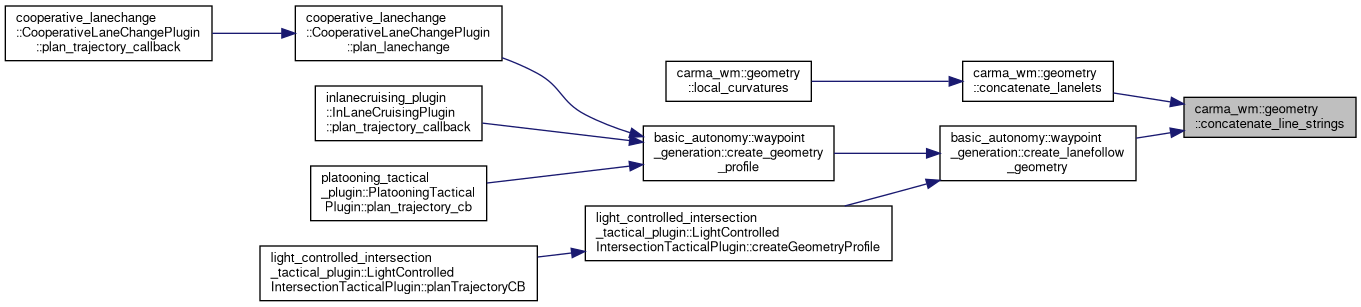
lanelet::BasicLineString2d	concatenate_line_strings (const lanelet::BasicLineString2d &l1, const lanelet::BasicLineString2d &l2)
	Helper function to concatenate 2 linestrings together and return the result. Neither LineString is modified in this function. More...
lanelet::BasicLineString2d	concatenate_lanelets (const std::vector< lanelet::ConstLanelet > &lanelets)
	Helper function to a list of lanelets together and return the result. Neither LineString is modified in this function. More...
std::vector< Eigen::Vector2d >	compute_finite_differences (const lanelet::BasicLineString2d &data)
	Use finite differences methods to compute the derivative of the input data set with respect to index Compute the finite differences using the forward finite difference for the first point, centered finite differences for the middle points and backwards finite difference for the final point. This will result in the middle points being a better approximation of the actual derivative than the endpoints. More...
std::vector< Eigen::Vector2d >	compute_finite_differences (const std::vector< lanelet::BasicPoint2d > &data)
std::vector< double >	compute_finite_differences (const std::vector< double > &data)
	Use finite differences methods to compute the derivative of the input data set with respect to index Compute the finite differences using the forward finite difference for the first point, centered finite differences for the middle points and backwards finite difference for the final point. This will result in the middle points being a better approximation of the actual derivative than the endpoints. More...
std::vector< Eigen::Vector2d >	compute_finite_differences (const std::vector< Eigen::Vector2d > &x, const std::vector< double > &y)
	Use finite differences methods to compute the derivative of the input data set with respect to the second paramter. More...
std::vector< double >	compute_arc_lengths (const std::vector< lanelet::BasicPoint2d > &data)
	Compute the arc length at each point around the curve. More...
std::vector< double >	compute_arc_lengths (const lanelet::BasicLineString2d &data)
	Compute the arc length at each point around the curve. More...
double	compute_euclidean_distance (const Eigen::Vector2d &a, const Eigen::Vector2d &b)
	Compute the Euclidean distance between the two points. More...
std::vector< Eigen::Vector2d >	normalize_vectors (const std::vector< Eigen::Vector2d > &vectors)
	Normalize the vectors in the input list such that their magnitudes = 1. More...
std::vector< double >	compute_magnitude_of_vectors (const std::vector< Eigen::Vector2d > &vectors)
	Compute the magnitude of each vector in the input list. More...
double	computeCurvature (const lanelet::BasicPoint2d &p1, const lanelet::BasicPoint2d &p2, const lanelet::BasicPoint2d &p3)
	Function for computing curvature from 3 points. More...
double	safeAcos (double x)
	acos method that caps the input x value for 1 or -1 to avoid undefined output. This is meant to prevent issues with floating point approximations. The user should still make sure the input data is expected to be within the [-1, 1] range for this method to give accurate results. More...
double	safeAsin (double x)
	asin method that caps the input x value for 1 or -1 to avoid undefined output. This is meant to prevent issues with floating point approximations. The user should still make sure the input data is expected to be within the [-1, 1] range for this method to give accurate results. More...
double	getAngleBetweenVectors (const Eigen::Vector2d &vec1, const Eigen::Vector2d &vec2)
	Calculates the angle between two vectors. More...
lanelet::BasicPolygon2d	objectToMapPolygon (const geometry_msgs::msg::Pose &pose, const geometry_msgs::msg::Vector3 &size)
	Uses the provided pose and size vector of an ExternalObject to compute what the polygon would be of that object would be if viewed from the same frame as the pose is defined relative to. More...
void	rpyFromQuaternion (const tf2::Quaternion &q, double &roll, double &pitch, double &yaw)
	Extract extrinsic roll-pitch-yaw from quaternion. More...
void	rpyFromQuaternion (const geometry_msgs::msg::Quaternion &q_msg, double &roll, double &pitch, double &yaw)
	Extract extrinsic roll-pitch-yaw from quaternion. More...
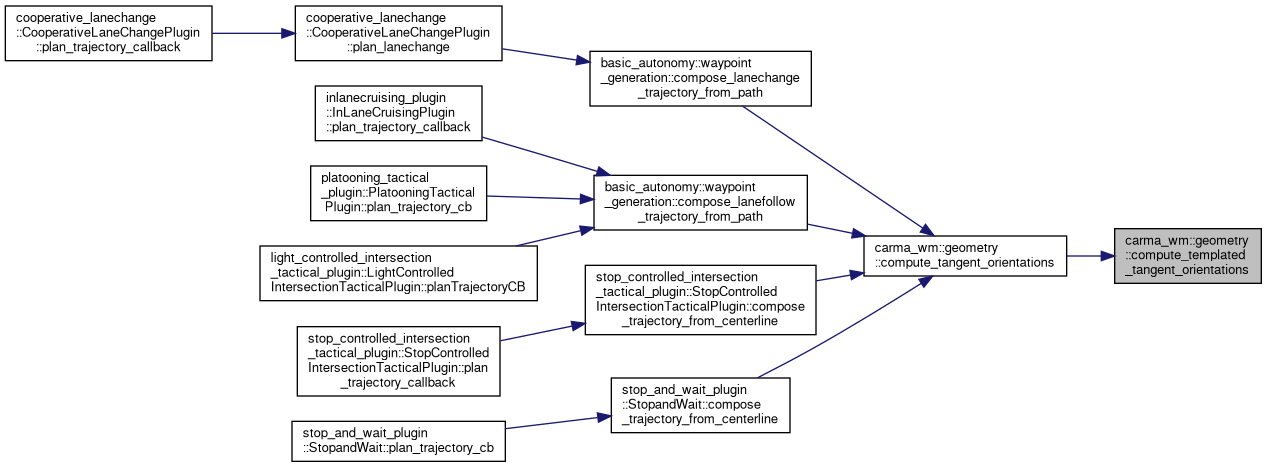
std::vector< double >	compute_tangent_orientations (const lanelet::BasicLineString2d &centerline)
	Compute an approximate orientation for the vehicle at each point along the provided centerline. More...
std::vector< double >	compute_tangent_orientations (const std::vector< lanelet::BasicPoint2d > &centerline)
Eigen::Isometry2d	build2dEigenTransform (const Eigen::Vector2d &position, const Eigen::Rotation2Dd &rotation)
	Builds a 2D Eigen coordinate frame transform with not applied scaling (only translation and rotation) based on the provided position and rotation parameters. More...
Eigen::Isometry3d	build3dEigenTransform (const Eigen::Vector3d &position, const Eigen::Quaterniond &rotation)
	Builds a 3D Eigen coordinate frame transform with not applied scaling (only translation and rotation) based on the provided position and rotation parameters. More...
Eigen::Isometry3d	build3dEigenTransform (const Eigen::Vector3d &position, const Eigen::AngleAxisd &rotation)
double	point_to_point_yaw (const lanelet::BasicPoint2d &cur_point, const lanelet::BasicPoint2d &next_point)
	Computes the 2d orientation of the vector from the provided start point to end point. More...
double	circular_arc_curvature (const lanelet::BasicPoint2d &cur_point, const lanelet::BasicPoint2d &next_point)
	Computes the curvature of a circular arc that passes through the two provided points. If the two points lie on a curve then larger distances between them will result in less accurate, but also less noisy curvature calculations. More...
std::vector< double >	local_circular_arc_curvatures (const std::vector< lanelet::BasicPoint2d > &points, int lookahead)
	Computes the curvature of each point in the provided list by calling circular_arc_curvature using that point and the point at index current point index + lookahead. In this way the curvature of a path is effectively low pass filtered by the size of the lookahead value. More...
bool	selectFirstSegment (const TrackPos &first_seg_trackPos, const TrackPos &second_seg_trackPos, double first_seg_length, double second_seg_length)
	Helper function to identify whether to select the preceeding or succeeding segment of a linstring point that is nearest an external point when trying to find the TrackPos of the external point. Of the 3 points comprising the 2 segment linestirng the external point must be closest to the midpoint for this function to be valid. More...
template<class P , class A >
std::vector< double >	templated_local_curvatures (const std::vector< P, A > &centerline_points)
template<class P , class A >
std::vector< Eigen::Vector2d >	compute_templated_finite_differences (const std::vector< P, A > &data)
template<class P , class A >
std::vector< double >	compute_templated_arc_lengths (const std::vector< P, A > &data)
template<class P , class A >
std::vector< double >	compute_templated_tangent_orientations (const std::vector< P, A > &centerline)

Variables
constexpr double	SPATIAL_EPSILON_M = 0.05

Detailed Description

geometry namespace contains utility geometry functions which do not require the map or route provided by an active world model

Function Documentation

build2dEigenTransform()

Eigen::Isometry2d carma_wm::geometry::build2dEigenTransform	(	const Eigen::Vector2d &	position,
		const Eigen::Rotation2Dd &	rotation
	)

Builds a 2D Eigen coordinate frame transform with not applied scaling (only translation and rotation) based on the provided position and rotation parameters.

Parameters

position	The origin of the child coordinate frame in the parent frame
rotation	The rotation of the child coordinate frame in the parent frame

Returns

A 2D transformation which is defined such that given a parent frame F and a child frame C, A point P_c in child frame C can be converted to the parent frame using the returned transform T_f_c Therefore P_f = T_f_c * P_c

Definition at line 570 of file Geometry.cpp.

                                                                                                       {
  Eigen::Vector2d scale(1.0, 1.0);
  Eigen::Isometry2d tf;
  return tf.fromPositionOrientationScale(position, rotation, scale);
}

Referenced by basic_autonomy::waypoint_generation::compute_heading_frame().

Here is the caller graph for this function:

build3dEigenTransform() [1/2]

Eigen::Isometry3d carma_wm::geometry::build3dEigenTransform	(	const Eigen::Vector3d &	position,
		const Eigen::AngleAxisd &	rotation
	)

Definition at line 582 of file Geometry.cpp.

                                                                                                      {
  Eigen::Vector3d scale(1.0, 1.0, 1.0);
  Eigen::Isometry3d tf;
  return tf.fromPositionOrientationScale(position, rotation, scale);
}

build3dEigenTransform() [2/2]

Eigen::Isometry3d carma_wm::geometry::build3dEigenTransform	(	const Eigen::Vector3d &	position,
		const Eigen::Quaterniond &	rotation
	)

Builds a 3D Eigen coordinate frame transform with not applied scaling (only translation and rotation) based on the provided position and rotation parameters.

Parameters

position	The origin of the child coordinate frame in the parent frame
rotation	The rotation of the child coordinate frame in the parent frame

Returns

A 3D transformation which is defined such that given a parent frame F and a child frame C, A point P_c in child frame C can be converted to the parent frame using the returned transform T_f_c Therefore P_f = T_f_c * P_c

Definition at line 576 of file Geometry.cpp.

                                                                                                       {
  Eigen::Vector3d scale(1.0, 1.0, 1.0);
  Eigen::Isometry3d tf;
  return tf.fromPositionOrientationScale(position, rotation, scale);
}

circular_arc_curvature()

double carma_wm::geometry::circular_arc_curvature	(	const lanelet::BasicPoint2d &	cur_point,
		const lanelet::BasicPoint2d &	next_point
	)

Computes the curvature of a circular arc that passes through the two provided points. If the two points lie on a curve then larger distances between them will result in less accurate, but also less noisy curvature calculations.

Parameters

cur_point	The first point
next_point	The second point

Returns

The curvature of the circular arc that passes through both points. Curvature is always positive.

Definition at line 596 of file Geometry.cpp.

{
  double dist = sqrt(pow(cur_point[0] - next_point[0], 2) + pow(cur_point[1] - next_point[1], 2));
 
  double angle = point_to_point_yaw(cur_point, next_point);
 
  double r = 0.5 * (dist / std::sin(angle));
 
  double max_curvature = 100000;
  double curvature = std::min(1 / r, max_curvature);
 
  return curvature;
}

References point_to_point_yaw().

Referenced by local_circular_arc_curvatures().

Here is the call graph for this function:

Here is the caller graph for this function:

compute_arc_lengths() [1/2]

std::vector< double > carma_wm::geometry::compute_arc_lengths

(

const lanelet::BasicLineString2d &

data

)

Compute the arc length at each point around the curve.

Definition at line 493 of file Geometry.cpp.

                                                          {
  return compute_templated_arc_lengths(data);
}

References compute_templated_arc_lengths(), and process_traj_logs::data.

Here is the call graph for this function:

compute_arc_lengths() [2/2]

std::vector< double > carma_wm::geometry::compute_arc_lengths

(

const std::vector< lanelet::BasicPoint2d > &

data

)

Compute the arc length at each point around the curve.

Definition at line 498 of file Geometry.cpp.

{
  return compute_templated_arc_lengths(data);
}

References compute_templated_arc_lengths(), and process_traj_logs::data.

Referenced by basic_autonomy::waypoint_generation::compose_lanechange_trajectory_from_path(), basic_autonomy::waypoint_generation::compose_lanefollow_trajectory_from_path(), stop_controlled_intersection_tactical_plugin::StopControlledIntersectionTacticalPlugin::compose_trajectory_from_centerline(), basic_autonomy::waypoint_generation::constrain_to_time_boundary(), basic_autonomy::waypoint_generation::resample_linestring_pair_to_same_size(), and templated_local_curvatures().

Here is the call graph for this function:

Here is the caller graph for this function:

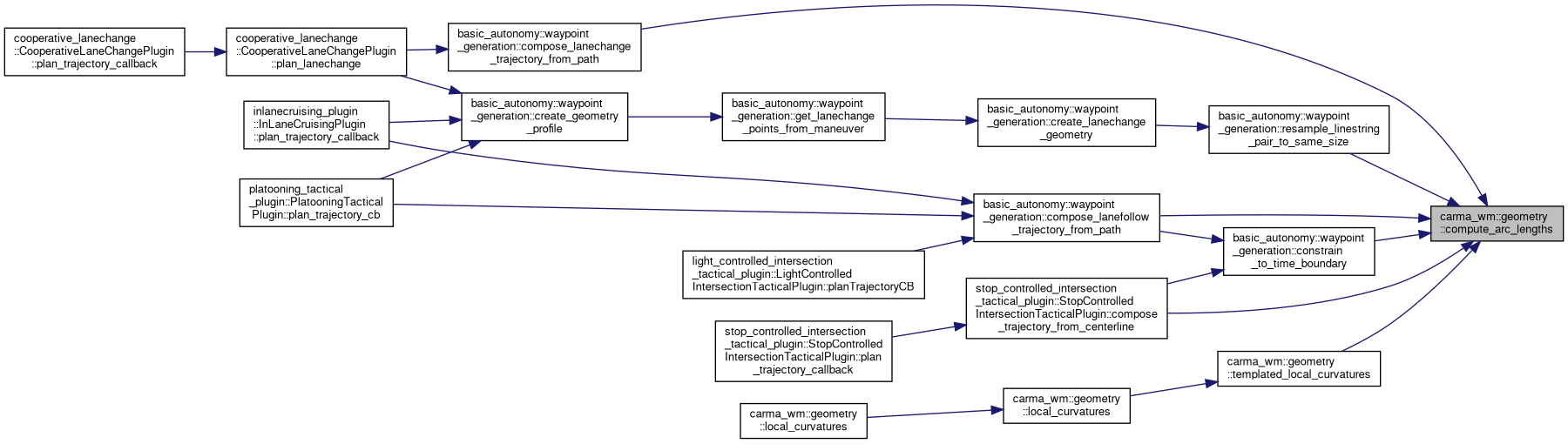
compute_euclidean_distance()

double carma_wm::geometry::compute_euclidean_distance	(	const Eigen::Vector2d &	a,
		const Eigen::Vector2d &	b
	)

Compute the Euclidean distance between the two points.

Definition at line 504 of file Geometry.cpp.

{
  return std::sqrt(std::pow(b[0] - a[0], 2) + std::pow(b[1] - a[1], 2));
}

Referenced by compute_templated_arc_lengths(), and concatenate_line_strings().

Here is the caller graph for this function:

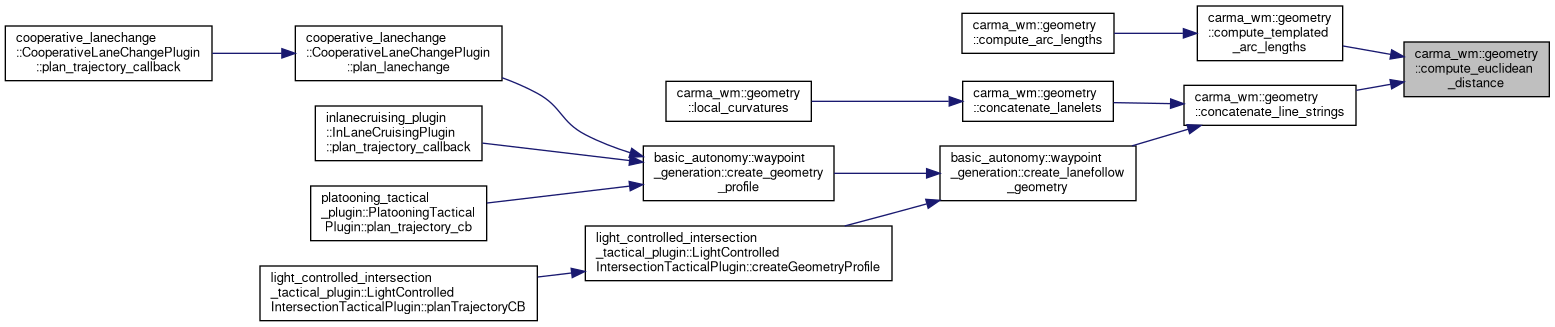
compute_finite_differences() [1/4]

std::vector< Eigen::Vector2d > carma_wm::geometry::compute_finite_differences

(

const lanelet::BasicLineString2d &

data

)

Use finite differences methods to compute the derivative of the input data set with respect to index Compute the finite differences using the forward finite difference for the first point, centered finite differences for the middle points and backwards finite difference for the final point. This will result in the middle points being a better approximation of the actual derivative than the endpoints.

Parameters

data	The data to differentiate over

Returns

A vector containing the point-by-point derivatives in the same indices as the input data

Definition at line 419 of file Geometry.cpp.

{
  return compute_templated_finite_differences(data);
}

References compute_templated_finite_differences(), and process_traj_logs::data.

Referenced by templated_local_curvatures().

Here is the call graph for this function:

Here is the caller graph for this function:

compute_finite_differences() [2/4]

std::vector< double > carma_wm::geometry::compute_finite_differences

(

const std::vector< double > &

data

)

Use finite differences methods to compute the derivative of the input data set with respect to index Compute the finite differences using the forward finite difference for the first point, centered finite differences for the middle points and backwards finite difference for the final point. This will result in the middle points being a better approximation of the actual derivative than the endpoints.

Parameters

data	The data to differentiate over

Returns

A vector containing the point-by-point derivatives in the same indices as the input data

Definition at line 429 of file Geometry.cpp.

{
  std::vector<double> out;
  double diff;
  for (size_t i = 0; i < data.size(); i++) {
 
    if (i == 0) {
      diff = data[i + 1] - data[i];
    } else if (i == data.size() - 1) {
      diff = data[i] - data[i - 1];
    } else {
      diff = (data[i + 1] - data[i - 1])/2.0;
    }
    
    out.push_back(diff);
  }
 
  return out;
}

References process_traj_logs::data, and process_bag::i.

compute_finite_differences() [3/4]

std::vector< Eigen::Vector2d > carma_wm::geometry::compute_finite_differences	(	const std::vector< Eigen::Vector2d > &	x,
		const std::vector< double > &	y
	)

Use finite differences methods to compute the derivative of the input data set with respect to the second paramter.

Input x and y must be the same length. Compute the finite differences using the forward finite difference for the first point, centered finite differences for the middle points and backwards finite difference for the final point. This will result in the middle points being a better approximation of the actual derivative than the endpoints.

Parameters

x	The x value of the derivative dx/dy
y	The y value of the derivative dx/dy

Returns

A vector containing the point-by-point derivatives in the same indices as the input data

Definition at line 450 of file Geometry.cpp.

{
  if (x.size() != y.size()) {
    throw std::invalid_argument("Attempting to differentiate two unequal sized lists!");
  }
 
  std::vector<Eigen::Vector2d> out;
  Eigen::Vector2d diff;
  for (size_t i = 0; i < x.size(); i++) {
    if (i == 0) {
      diff = (x[i + 1] - x[i])/(y[i + 1] - y[i]);
    } else if (i == x.size() - 1) {
      diff = (x[i] - x[i - 1])/(y[i] - y[i - 1]);
    } else {
      diff = (x[i + 1] - x[i - 1])/(y[i + 1] - y[i - 1]);
    }
    
    out.push_back(diff);
  }
 
  return out;
}

References process_bag::i, process_traj_logs::x, and process_traj_logs::y.

compute_finite_differences() [4/4]

std::vector< Eigen::Vector2d > carma_wm::geometry::compute_finite_differences

(

const std::vector< lanelet::BasicPoint2d > &

data

)

Definition at line 424 of file Geometry.cpp.

                                                                                                {
  return compute_templated_finite_differences(data);
}

References compute_templated_finite_differences(), and process_traj_logs::data.

Here is the call graph for this function:

compute_magnitude_of_vectors()

std::vector< double > carma_wm::geometry::compute_magnitude_of_vectors

(

const std::vector< Eigen::Vector2d > &

vectors

)

Compute the magnitude of each vector in the input list.

Definition at line 520 of file Geometry.cpp.

{
  std::vector<double> out;
  for (auto vec : vectors) {
    out.push_back(vec.norm());
  }
 
  return out;
}

Referenced by templated_local_curvatures().

Here is the caller graph for this function:

compute_tangent_orientations() [1/2]

std::vector< double > carma_wm::geometry::compute_tangent_orientations

(

const lanelet::BasicLineString2d &

centerline

)

Compute an approximate orientation for the vehicle at each point along the provided centerline.

!

Uses the tangent vectors along the centerline to estimate vehicle pose in the yaw dimension. Roll and pitch are not considered.

Parameters

centerline

centerline represented as BasicLinestring2d to compute the orientation

Returns

A vector of doubles representing the yaw value in radians the same frame as the provided centerline.

Definition at line 559 of file Geometry.cpp.

{
  return compute_templated_tangent_orientations(centerline);
}

References compute_templated_tangent_orientations().

Referenced by basic_autonomy::waypoint_generation::compose_lanechange_trajectory_from_path(), basic_autonomy::waypoint_generation::compose_lanefollow_trajectory_from_path(), stop_controlled_intersection_tactical_plugin::StopControlledIntersectionTacticalPlugin::compose_trajectory_from_centerline(), and stop_and_wait_plugin::StopandWait::compose_trajectory_from_centerline().

Here is the call graph for this function:

Here is the caller graph for this function:

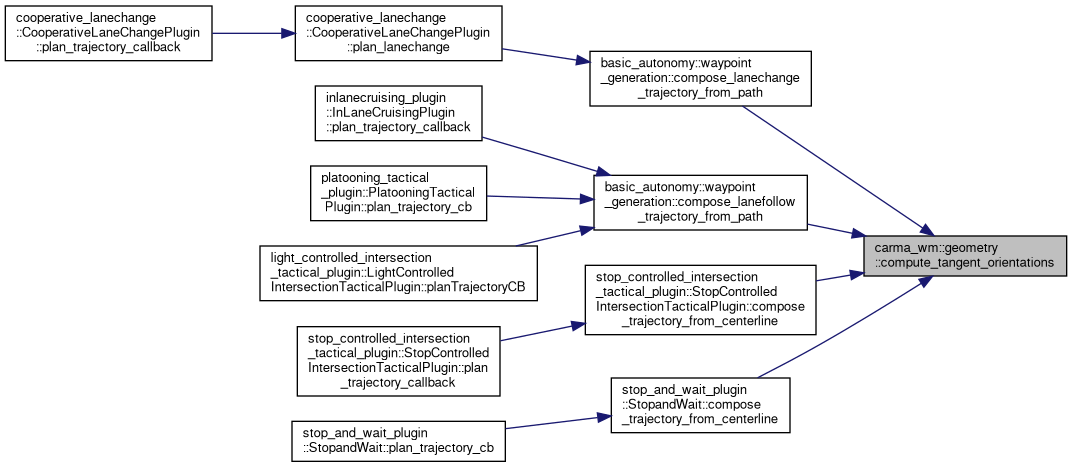
compute_tangent_orientations() [2/2]

std::vector< double > carma_wm::geometry::compute_tangent_orientations

(

const std::vector< lanelet::BasicPoint2d > &

centerline

)

Definition at line 565 of file Geometry.cpp.

{
  return compute_templated_tangent_orientations(centerline);
}

References compute_templated_tangent_orientations().

Here is the call graph for this function:

compute_templated_arc_lengths()

template<class P , class A >

std::vector< double > carma_wm::geometry::compute_templated_arc_lengths

(

const std::vector< P, A > &

data

)

Definition at line 475 of file Geometry.cpp.

                                                           {
  std::vector<double> out;
  double total = 0;
  double diff = 0;
  for (size_t i =  0; i < data.size(); i++) {
    if (i == 0) {
      out.push_back(0);
    } else {
      diff = compute_euclidean_distance(data[i - 1], data[i]);
      total += diff;
      out.push_back(total);
    }
  }
 
  return out;
}

References compute_euclidean_distance(), process_traj_logs::data, and process_bag::i.

Referenced by compute_arc_lengths().

Here is the call graph for this function:

Here is the caller graph for this function:

compute_templated_finite_differences()

template<class P , class A >

std::vector< Eigen::Vector2d > carma_wm::geometry::compute_templated_finite_differences

(

const std::vector< P, A > &

data

)

Definition at line 391 of file Geometry.cpp.

{
  std::vector<Eigen::Vector2d> out;
  Eigen::Vector2d diff;
  Eigen::Vector2d vec_i_plus_1;
  Eigen::Vector2d vec_i_minus_1;
 
  for (size_t i = 0; i < data.size(); i++) {
    if (i == 0) {
      // Compute forward derivative
      diff = (data[i + 1] - data[i]);
    } else if (i == data.size() - 1) {
      // Compute backward derivative
      diff = (data[i] - data[i - 1]);
    } else {
      // Else, compute centered derivative
      vec_i_plus_1 = data[i + 1];
      vec_i_minus_1 = data[i - 1];
      diff = (vec_i_plus_1 - vec_i_minus_1)/2.0;
    }
 
    out.push_back(diff);
  }
 
  return out;
}

References process_traj_logs::data, and process_bag::i.

Referenced by compute_finite_differences(), and compute_templated_tangent_orientations().

Here is the caller graph for this function:

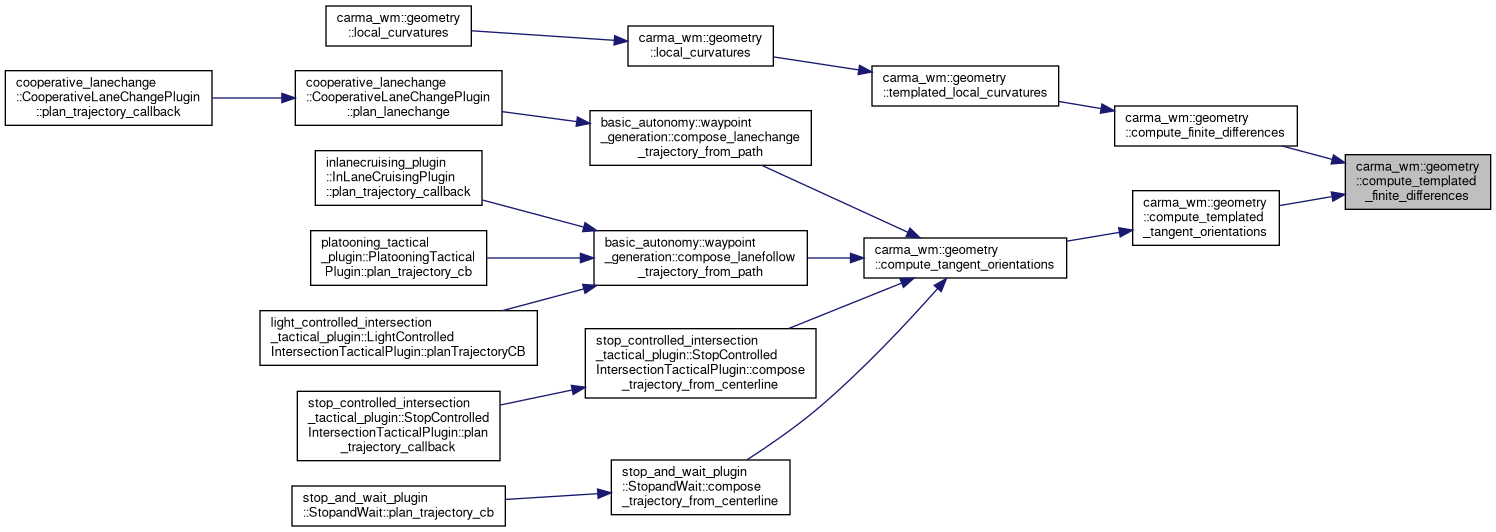
compute_templated_tangent_orientations()

template<class P , class A >

std::vector< double > carma_wm::geometry::compute_templated_tangent_orientations

(

const std::vector< P, A > &

centerline

)

Definition at line 532 of file Geometry.cpp.

{
  std::vector<double> out;
  if (centerline.empty())
    return out;
 
  std::vector<Eigen::Vector2d> tangents = carma_wm::geometry::compute_templated_finite_differences(centerline);
 
  for (auto tangent : tangents)
  {
    geometry_msgs::msg::Quaternion q;
 
    // Derive angle by cos theta = (u . v)/(||u| * ||v||)
    double yaw = 0;
    double norm = tangent.norm();
    if (norm != 0.0) {
      auto normalized_tanged = tangent / norm;
      yaw = atan2(normalized_tanged[1], normalized_tanged[0]);
    }
 
    out.push_back(yaw);
  }
 
  return out;
}

References compute_templated_finite_differences().

Referenced by compute_tangent_orientations().

Here is the call graph for this function:

Here is the caller graph for this function:

computeCurvature()

double carma_wm::geometry::computeCurvature	(	const lanelet::BasicPoint2d &	p1,
		const lanelet::BasicPoint2d &	p2,
		const lanelet::BasicPoint2d &	p3
	)

Function for computing curvature from 3 points.

This function is a direct copy of the function by the same name found in the lanelet2_validation package which was not exposed for use The original function can be found here https://github.com/fzi-forschungszentrum-informatik/Lanelet2/blob/master/lanelet2_validation/src/validators/CurvatureTooBig.cpp The source function is copyrighted under BSD 3-Clause "New" or "Revised" License a copy of that notice has been included with this package

Parameters

p1	The first point
p2	The second point
p3	The third point

Returns

The computed curvature in 1/m units.

Definition at line 276 of file Geometry.cpp.

{
  auto dp = 0.5 * (p3 - p1);
  auto ddp = p3 - 2.0 * p2 + p1;
  auto denom = std::pow(dp.x() * dp.x() + dp.y() * dp.y(), 3.0 / 2.0);
  if (std::fabs(denom) < 1e-20)
  {
    denom = 1e-20;
  }
  return static_cast<double>((ddp.y() * dp.x() - dp.y() * ddp.x()) / denom);
}

concatenate_lanelets()

lanelet::BasicLineString2d carma_wm::geometry::concatenate_lanelets

(

const std::vector< lanelet::ConstLanelet > &

lanelets

)

Helper function to a list of lanelets together and return the result. Neither LineString is modified in this function.

Definition at line 316 of file Geometry.cpp.

{
  if (lanelets.empty()) {
    return lanelet::BasicLineString2d();
  }
  lanelet::BasicLineString2d centerline_points = lanelets[0].centerline2d().basicLineString();
  lanelet::BasicLineString2d new_points;
  for (size_t i = 1; i < lanelets.size(); i++) {
    new_points = lanelets[i].centerline2d().basicLineString();
    centerline_points = concatenate_line_strings(centerline_points, new_points);
  }
 
  return centerline_points;
}

References concatenate_line_strings(), and process_bag::i.

Referenced by local_curvatures().

Here is the call graph for this function:

Here is the caller graph for this function:

concatenate_line_strings()

lanelet::BasicLineString2d carma_wm::geometry::concatenate_line_strings	(	const lanelet::BasicLineString2d &	l1,
		const lanelet::BasicLineString2d &	l2
	)

Helper function to concatenate 2 linestrings together and return the result. Neither LineString is modified in this function.

Definition at line 373 of file Geometry.cpp.

{
  lanelet::BasicLineString2d out;
 
  int start_offset = 0;
  if (!a.empty() && !b.empty() && compute_euclidean_distance(a.back(), b.front()) < SPATIAL_EPSILON_M) {
    start_offset = 1;
  }
 
  out.insert(out.end(), a.begin(), a.end());
  out.insert(out.end(), b.begin() + start_offset, b.end());
 
  return out;
}

References compute_euclidean_distance(), and SPATIAL_EPSILON_M.

Referenced by concatenate_lanelets(), and basic_autonomy::waypoint_generation::create_lanefollow_geometry().

Here is the call graph for this function:

Here is the caller graph for this function:

getAngleBetweenVectors()

double carma_wm::geometry::getAngleBetweenVectors	(	const Eigen::Vector2d &	vec1,
		const Eigen::Vector2d &	vec2
	)

Calculates the angle between two vectors.

Parameters

vec1	the first vector
vec2	the second vector

Returns

The angle in rad between the two vectors

Definition at line 65 of file Geometry.cpp.

{
  double vec1Mag = vec1.norm();
  double vec2Mag = vec2.norm();
  if (vec1Mag == 0.0 || vec2Mag == 0.0)
  {
    return 0;
  }
  return safeAcos(vec1.dot(vec2) / (vec1Mag * vec2Mag));
}

References safeAcos().

Referenced by carma_wm::query::getAffectedLaneletOrAreas(), and trackPos().

Here is the call graph for this function:

Here is the caller graph for this function:

local_circular_arc_curvatures()

std::vector< double > carma_wm::geometry::local_circular_arc_curvatures	(	const std::vector< lanelet::BasicPoint2d > &	points,
		int	lookahead
	)

Computes the curvature of each point in the provided list by calling circular_arc_curvature using that point and the point at index current point index + lookahead. In this way the curvature of a path is effectively low pass filtered by the size of the lookahead value.

Parameters

points	The points to compute the curvature for
lookahead	The lookahead index distance to use for computing the curvature at each point

Returns

A vector of computed curvatures that has size equal to points.size()

Definition at line 610 of file Geometry.cpp.

                                                                                                             {
  std::vector<double> curvatures;
  curvatures.reserve(points.size());
 
  if (lookahead <= 0) {
    throw std::invalid_argument("local_circular_arc_curvatures lookahead must be greater than 0");
  }
 
  if (points.empty()) {
    return curvatures;
  }
  else if (points.size() == 1) {
    curvatures.push_back(0.0);
    return curvatures;
  }
 
  for (size_t i = 0; i < points.size() - 1; i++)
  {
    size_t next_point_index = i + lookahead;
    if (next_point_index >= points.size()) {
      next_point_index = points.size() - 1;
    }
    double cur = circular_arc_curvature(points[i], points[next_point_index]);
    curvatures.push_back(fabs(cur));
  }
  curvatures.push_back(curvatures.back());
  return curvatures;
}

References circular_arc_curvature(), and process_bag::i.

Here is the call graph for this function:

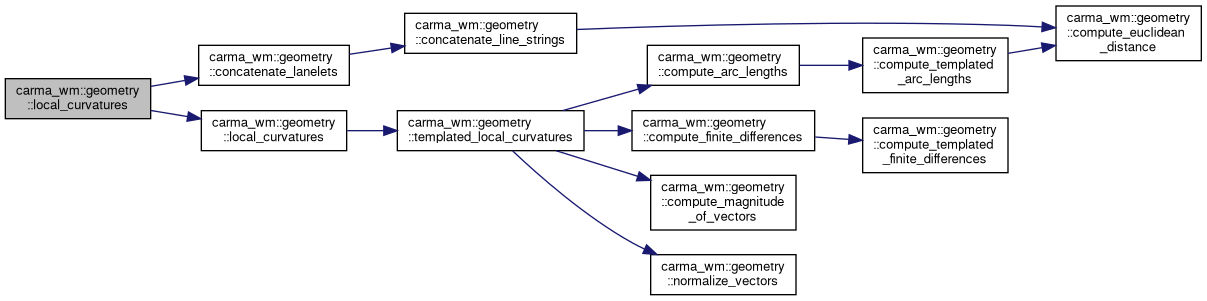
local_curvatures() [1/3]

std::vector< double > carma_wm::geometry::local_curvatures

(

const lanelet::BasicLineString2d &

centerline_points

)

Returns a list of local (computed by discrete derivative) curvatures for the input centerlines. The list of returned curvatures matches 1-to-1 with with list of points in the input centerlines.

The numerical accuracy of this method is greatly increased by using larger collections of points as inputs as the first 2 and final 2 points in the list must be computed using alternative differentiation methods from all the others resulting in greater error. It is also important for this function to yield useful results that all points in the input lanelet's centerline are actually on the centerline of the lanelet (i.e. none to minimal linear interpolation of points) as this results in "flat" spots on an otherwise smooth curve that causes 0 curvature to be computed.

NOTE: The accuracy of this method is very susceptable to input noise. Consider using local_circular_arc_curvatures for calculations using noisy data

Parameters

centerline_points

The list of points to compute curvatures for

Exceptions

std::invalid_argument

If one of the provided lanelets cannot have its centerline computed

Returns

A list of continuous centerline segments and their respective curvatures

Definition at line 356 of file Geometry.cpp.

{
  return templated_local_curvatures(centerline_points);
}

References templated_local_curvatures().

Referenced by local_curvatures().

Here is the call graph for this function:

Here is the caller graph for this function:

local_curvatures() [2/3]

std::vector< double > carma_wm::geometry::local_curvatures

(

const std::vector< lanelet::BasicPoint2d > &

centerline_points

)

Definition at line 362 of file Geometry.cpp.

{
  return templated_local_curvatures(centerline_points);
}

References templated_local_curvatures().

Here is the call graph for this function:

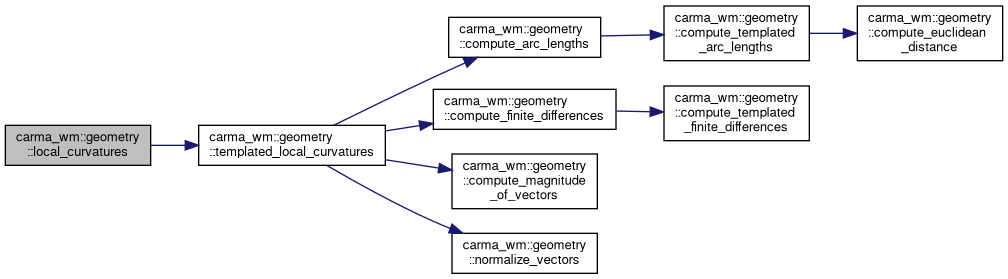
local_curvatures() [3/3]

std::vector< double > carma_wm::geometry::local_curvatures

(

const std::vector< lanelet::ConstLanelet > &

lanelets

)

Specialized overload of the centerline local_curvatures method but for lanelets.

Parameters

lanelets

The list of points to compute curvatures for

Exceptions

std::invalid_argument

If one of the provided lanelets cannot have its centerline computed

Definition at line 368 of file Geometry.cpp.

                                                                 {
  return local_curvatures(concatenate_lanelets(lanelets));
}

References concatenate_lanelets(), and local_curvatures().

Here is the call graph for this function:

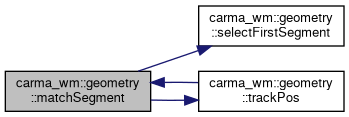
matchSegment()

std::tuple< TrackPos, lanelet::BasicSegment2d > carma_wm::geometry::matchSegment	(	const lanelet::BasicPoint2d &	p,
		const lanelet::BasicLineString2d &	line_string
	)

Get the TrackPos of the provided point along the linestring and the segment of the line string which the provided point should be considered in.

This function iterates over the provided linestring from front to back. First the nearest vertex point on the linestring to the external point is found Once the nearest point has been found next step is to determine which segment it should go with using the following rules. If the minimum point is the first point then use the first segment If the minimum point is the last point then use the last segment If the minimum point is within the downtrack bounds of one segment but not the other then use the one it is within If the minimum point is within the downtrack bounds of both segments then use the one with the smallest crosstrack distance If the minimum point is within the downtrack bounds of both segments and has exactly equal crosstrack bounds with each segment then use the first one

Parameters

point	The 2d point to match with a segment
line_string	The line_string to match against

Exceptions

std::invalid_argument

if line string contains only one point

Returns

An std::tuple where the first element is the TrackPos of the point and the second element is the matched segment

Definition at line 187 of file Geometry.cpp.

{
  if (line_string.size() < 2)
  {
    throw std::invalid_argument("Provided with linestring containing fewer than 2 points");
  }
 
  lanelet::BasicSegment2d best_segment =
      std::make_pair(line_string[0], line_string[1]);  // Default to starting segment if no match is found
  auto point_2d = lanelet::utils::to2D(p);
 
  double min_distance = lanelet::geometry::distance2d(point_2d, line_string[0]);
  size_t best_point_index = 0;
  double best_accumulated_length = 0;
  double best_last_accumulated_length = 0;
  double best_seg_length = 0;
  double best_last_seg_length = 0;
  double last_seg_length = 0;
 
  double accumulated_length = 0;
  double last_accumulated_length = 0;
  for (size_t i = 0; i < line_string.size(); i++)
  {  // Iterate over line string to find nearest point
    double seg_length = 0;
    if (i < line_string.size() - 1)
    {
      seg_length = lanelet::geometry::distance2d(line_string[i], line_string[i + 1]);  // Compute segment length
    }
 
    double distance = lanelet::geometry::distance2d(p, line_string[i]);  // Compute from current point to external point
    if (distance < min_distance)
    {  // If this distance is below minimum discovered so far then update minimum
      min_distance = distance;
      best_point_index = i;
      best_accumulated_length = accumulated_length;
      best_last_accumulated_length = last_accumulated_length;  // Record accumulated lengths to each segment
      best_seg_length = seg_length;
      best_last_seg_length = last_seg_length;
    }
 
    last_accumulated_length = accumulated_length;  // Update accumulated lenths
    accumulated_length += seg_length;
    last_seg_length = seg_length;
  }
 
  // Minimum point has been found next step is to determine which segment it should go with using the following rules.
  // If the minimum point is the first point then use the first segment
  // If the minimum point is the last point then use the last segment
  // If the minimum point is within the downtrack bounds of one segment but not the other then use the one it is within
  // If the minimum point is within the downtrack bounds of both segments then use the one with the smallest crosstrack
  // distance If the minimum point is within the downtrack bounds of both segments and has exactly equal crosstrack
  // bounds with each segment then use the first one
  TrackPos best_pos(0, 0);
  if (best_point_index == 0)
  {
    best_pos = trackPos(p, line_string[0], line_string[1]);
    best_segment = std::make_pair(line_string[0], line_string[1]);
  }
  else if (best_point_index == line_string.size() - 1)
  {
    best_pos = trackPos(p, line_string[line_string.size() - 2], line_string[line_string.size() - 1]);
    best_pos.downtrack += best_last_accumulated_length;
    best_segment = std::make_pair(line_string[line_string.size() - 2], line_string[line_string.size() - 1]);
  }
  else
  {
    TrackPos first_seg_trackPos = trackPos(p, line_string[best_point_index - 1], line_string[best_point_index]);
    TrackPos second_seg_trackPos = trackPos(p, line_string[best_point_index], line_string[best_point_index + 1]);
    if (selectFirstSegment(first_seg_trackPos, second_seg_trackPos, best_last_seg_length, best_seg_length))
    {
      best_pos = first_seg_trackPos;
      best_pos.downtrack += best_last_accumulated_length;
      best_segment = std::make_pair(line_string[best_point_index - 1], line_string[best_point_index]);
    }
    else
    {
      best_pos = second_seg_trackPos;
      best_pos.downtrack += best_accumulated_length;
      best_segment = std::make_pair(line_string[best_point_index], line_string[best_point_index + 1]);
    }
  }
 
  // couldn't find a matching segment, so use the first segment within the downtrack range of.
  // Or the starting segment assuming we are before the route
  return std::make_tuple(best_pos, best_segment);
}

References carma_wm::TrackPos::downtrack, process_bag::i, selectFirstSegment(), and trackPos().

Referenced by carma_wm::CARMAWorldModel::routeTrackPos(), and trackPos().

Here is the call graph for this function:

Here is the caller graph for this function:

normalize_vectors()

std::vector< Eigen::Vector2d > carma_wm::geometry::normalize_vectors

(

const std::vector< Eigen::Vector2d > &

vectors

)

Normalize the vectors in the input list such that their magnitudes = 1.

Definition at line 510 of file Geometry.cpp.

{
  std::vector<Eigen::Vector2d> out;
  for (auto vec : vectors) {
    out.push_back(vec.normalized());
  }
  return out;
}

Referenced by templated_local_curvatures().

Here is the caller graph for this function:

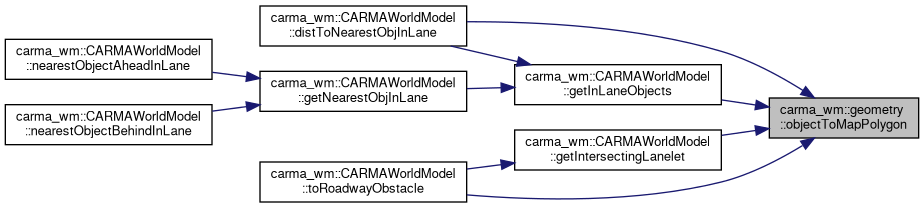
objectToMapPolygon()

lanelet::BasicPolygon2d carma_wm::geometry::objectToMapPolygon	(	const geometry_msgs::msg::Pose &	pose,
		const geometry_msgs::msg::Vector3 &	size
	)

Uses the provided pose and size vector of an ExternalObject to compute what the polygon would be of that object would be if viewed from the same frame as the pose is defined relative to.

Parameters

pose	the pose of an external object
size	The size vector of an external object

Returns

A polygon of 4 points describing the object aligned bounds starting with the upper left point in the object frame and moving clockwise.

Definition at line 289 of file Geometry.cpp.

{
  tf2::Transform object_tf;
  tf2::fromMsg(pose, object_tf);
 
  double half_x_bound = size.x / 2;
  double half_y_bound = size.y / 2;
 
  // 4 corners of the object starting with upper left and moving in clockwise direction in pose frame
  tf2::Vector3 obj_p1(half_x_bound, half_y_bound, 0);
  tf2::Vector3 obj_p2(half_x_bound, -half_y_bound, 0);
  tf2::Vector3 obj_p3(-half_x_bound, -half_y_bound, 0);
  tf2::Vector3 obj_p4(-half_x_bound, half_y_bound, 0);
 
  tf2::Vector3 obj_p1_map = object_tf * obj_p1;
  tf2::Vector3 obj_p2_map = object_tf * obj_p2;
  tf2::Vector3 obj_p3_map = object_tf * obj_p3;
  tf2::Vector3 obj_p4_map = object_tf * obj_p4;
 
  lanelet::BasicPoint2d p1(obj_p1_map.getX(), obj_p1_map.getY());
  lanelet::BasicPoint2d p2(obj_p2_map.getX(), obj_p2_map.getY());
  lanelet::BasicPoint2d p3(obj_p3_map.getX(), obj_p3_map.getY());
  lanelet::BasicPoint2d p4(obj_p4_map.getX(), obj_p4_map.getY());
 
  return { p1, p2, p3, p4 };
}

Referenced by carma_wm::CARMAWorldModel::distToNearestObjInLane(), carma_wm::CARMAWorldModel::getInLaneObjects(), carma_wm::CARMAWorldModel::getIntersectingLanelet(), and carma_wm::CARMAWorldModel::toRoadwayObstacle().

Here is the caller graph for this function:

point_to_point_yaw()

double carma_wm::geometry::point_to_point_yaw	(	const lanelet::BasicPoint2d &	cur_point,
		const lanelet::BasicPoint2d &	next_point
	)

Computes the 2d orientation of the vector from the provided start point to end point.

Parameters

cur_point	The start point of the orientation vector. Units m
next_point	The end point of the orientation vector. Units m

Returns

The rotation of the vector around the +Z axis in radians

Definition at line 588 of file Geometry.cpp.

{
  double dx = next_point[0] - cur_point[0];
  double dy = next_point[1] - cur_point[1];
  double yaw = atan2(dy, dx);
  return yaw;
}

Referenced by circular_arc_curvature(), and carma_wm::CARMAWorldModel::pointFromRouteTrackPos().

Here is the caller graph for this function:

rpyFromQuaternion() [1/2]

void carma_wm::geometry::rpyFromQuaternion	(	const geometry_msgs::msg::Quaternion &	q_msg,
		double &	roll,
		double &	pitch,
		double &	yaw
	)

Extract extrinsic roll-pitch-yaw from quaternion.

Parameters

q	The quaternion message to convert
roll	The output variable for roll units will be radians
pitch	The output variable for pitch units will be radians
yaw	The output variable for yaw units will be radians

Definition at line 58 of file Geometry.cpp.

{
  tf2::Quaternion quat;
  tf2::convert(q_msg, quat);
  rpyFromQuaternion(quat, roll, pitch, yaw);
}

References motion_computation::conversion::convert(), and rpyFromQuaternion().

Here is the call graph for this function:

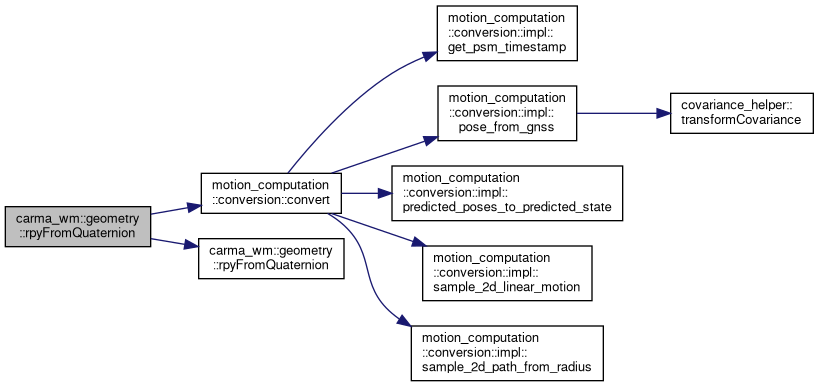
rpyFromQuaternion() [2/2]

void carma_wm::geometry::rpyFromQuaternion	(	const tf2::Quaternion &	q,
		double &	roll,
		double &	pitch,
		double &	yaw
	)

Extract extrinsic roll-pitch-yaw from quaternion.

Parameters

q	The quaternion to convert
roll	The output variable for roll units will be radians
pitch	The output variable for pitch units will be radians
yaw	The output variable for yaw units will be radians

Definition at line 52 of file Geometry.cpp.

{
  tf2::Matrix3x3 mat(q);
  mat.getRPY(roll, pitch, yaw);
}

Referenced by plan_delegator::PlanDelegator::composePlanTrajectoryRequest(), and rpyFromQuaternion().

Here is the caller graph for this function:

safeAcos()

double carma_wm::geometry::safeAcos

(

double

x

)

acos method that caps the input x value for 1 or -1 to avoid undefined output. This is meant to prevent issues with floating point approximations. The user should still make sure the input data is expected to be within the [-1, 1] range for this method to give accurate results.

Parameters

x	The angle in radians

Returns

The arc cosine of x

Definition at line 34 of file Geometry.cpp.

{
  if (x < -1.0) x = -1.0 ;
  else if (x > 1.0) x = 1.0 ;
  return std::acos(x) ;
}

References process_traj_logs::x.

Referenced by getAngleBetweenVectors().

Here is the caller graph for this function:

safeAsin()

double carma_wm::geometry::safeAsin

(

double

x

)

asin method that caps the input x value for 1 or -1 to avoid undefined output. This is meant to prevent issues with floating point approximations. The user should still make sure the input data is expected to be within the [-1, 1] range for this method to give accurate results.

Parameters

x	The angle in radians

Returns

The arc sine of x

Definition at line 45 of file Geometry.cpp.

{
  if (x < -1.0) x = -1.0 ;
  else if (x > 1.0) x = 1.0 ;
  return std::asin(x) ;
}

References process_traj_logs::x.

selectFirstSegment()

bool carma_wm::geometry::selectFirstSegment	(	const TrackPos &	first_seg_trackPos,
		const TrackPos &	second_seg_trackPos,
		double	first_seg_length,
		double	second_seg_length
	)

Helper function to identify whether to select the preceeding or succeeding segment of a linstring point that is nearest an external point when trying to find the TrackPos of the external point. Of the 3 points comprising the 2 segment linestirng the external point must be closest to the midpoint for this function to be valid.

ASSUMPTION: Of the 3 points comprising the 2 segment linestirng the external point is closest to the midpoint

Meant to be called in the matchSegment method. Logic is as follows If the external point is within the downtrack bounds of one segment but not the other then use the one it is within If the external point is within the downtrack bounds of both segments then use the one with the smallest crosstrack distance If the external point is within the downtrack bounds of both segments and has exactly equal crosstrack bounds with each segment then use the preceeding segment If the external point is outside the downtrack bounds of both segments then assign to the first segment as it will always have positive downtrack in this case while the second segment will always have negative downtrack

Parameters

first_seg_trackPos	The TrackPos of the external point relative to the preceeding segment
second_seg_trackPos	The TrackPos of the succeeding segment
first_seg_length	The length of the preceeding segment
second_seg_length	The length of the succeeding segment

Returns

True if the preceeding segment is the better choice. False if the succeeding segment is the better choice.

Definition at line 156 of file Geometry.cpp.

{
  const bool first_seg_in_downtrack =
      (0 <= first_seg_trackPos.downtrack && first_seg_trackPos.downtrack < first_seg_length);
  const bool second_seg_in_downtrack =
      (0 <= second_seg_trackPos.downtrack && second_seg_trackPos.downtrack < second_seg_length);
 
  if (first_seg_in_downtrack && !second_seg_in_downtrack)
  {  // If in the first segment but not the last segment
 
    return true;  // First segment is better
  }
  else if (second_seg_in_downtrack && !first_seg_in_downtrack)
  {
    return false;  // Second segment is better
  }
  else if (first_seg_in_downtrack && second_seg_in_downtrack)
  {
    return first_seg_trackPos.crosstrack <=
           second_seg_trackPos.crosstrack;  // Pick the first segment if the crosstrack values are equal or the first
                                            // segment is closer
  }
  else
  {  // Point lies outside the downtrack bounds of both segments (Remember According to function contract the nearest
     // point to external point is the midpoint of the two segments)
    return true;  // Choose first segment as it will always have positive downtrack in this case while the second
                  // segment will always have negative downtrack
  }
}

References carma_wm::TrackPos::crosstrack, and carma_wm::TrackPos::downtrack.

Referenced by matchSegment().

Here is the caller graph for this function:

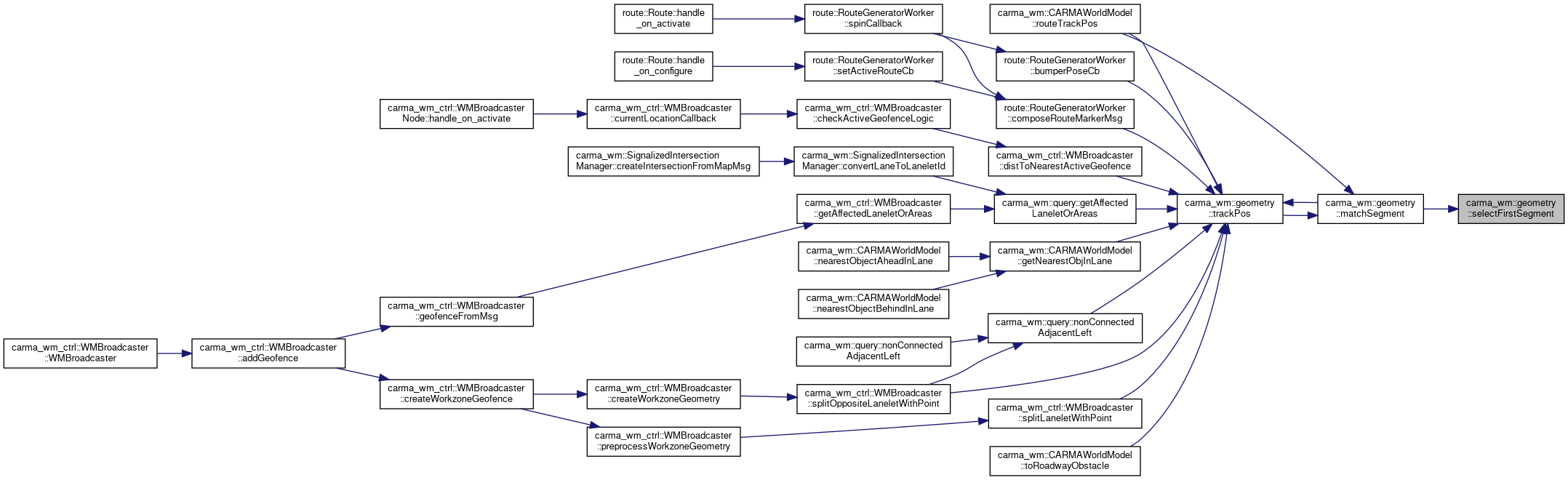
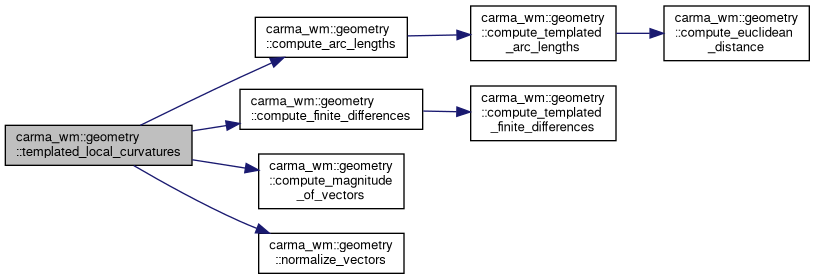
templated_local_curvatures()

template<class P , class A >

std::vector< double > carma_wm::geometry::templated_local_curvatures

(

const std::vector< P, A > &

centerline_points

)

Definition at line 333 of file Geometry.cpp.

{
 
  if (centerline_points.empty()) {
    throw std::invalid_argument("No points in centerline for curvature calculation");
  }
 
  std::vector<Eigen::Vector2d> spatial_derivative = compute_finite_differences(centerline_points);
  std::vector<Eigen::Vector2d> normalized_tangent_vectors = normalize_vectors(spatial_derivative);
 
  std::vector<double> arc_lengths = compute_arc_lengths(centerline_points);
 
  std::vector<Eigen::Vector2d> tangent_derivative = 
    compute_finite_differences(
      normalized_tangent_vectors, 
      arc_lengths);
 
  std::vector<double> curvature = compute_magnitude_of_vectors(tangent_derivative);
 
  return curvature;
}

References compute_arc_lengths(), compute_finite_differences(), compute_magnitude_of_vectors(), and normalize_vectors().

Referenced by local_curvatures().

Here is the call graph for this function:

Here is the caller graph for this function:

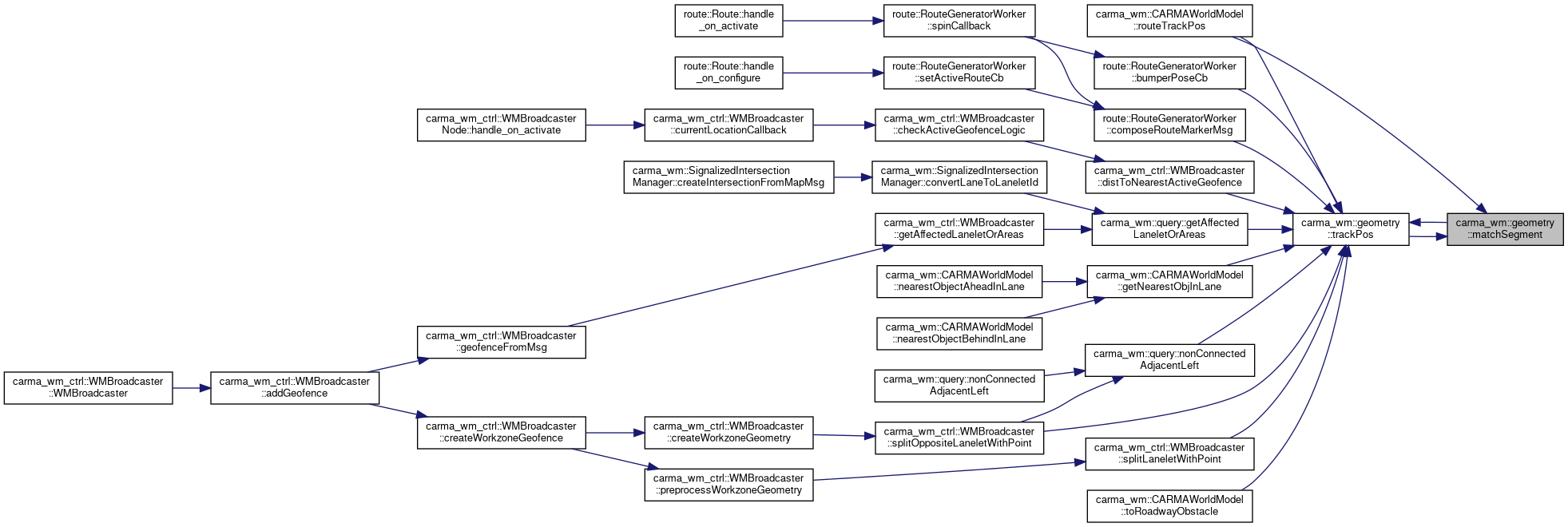
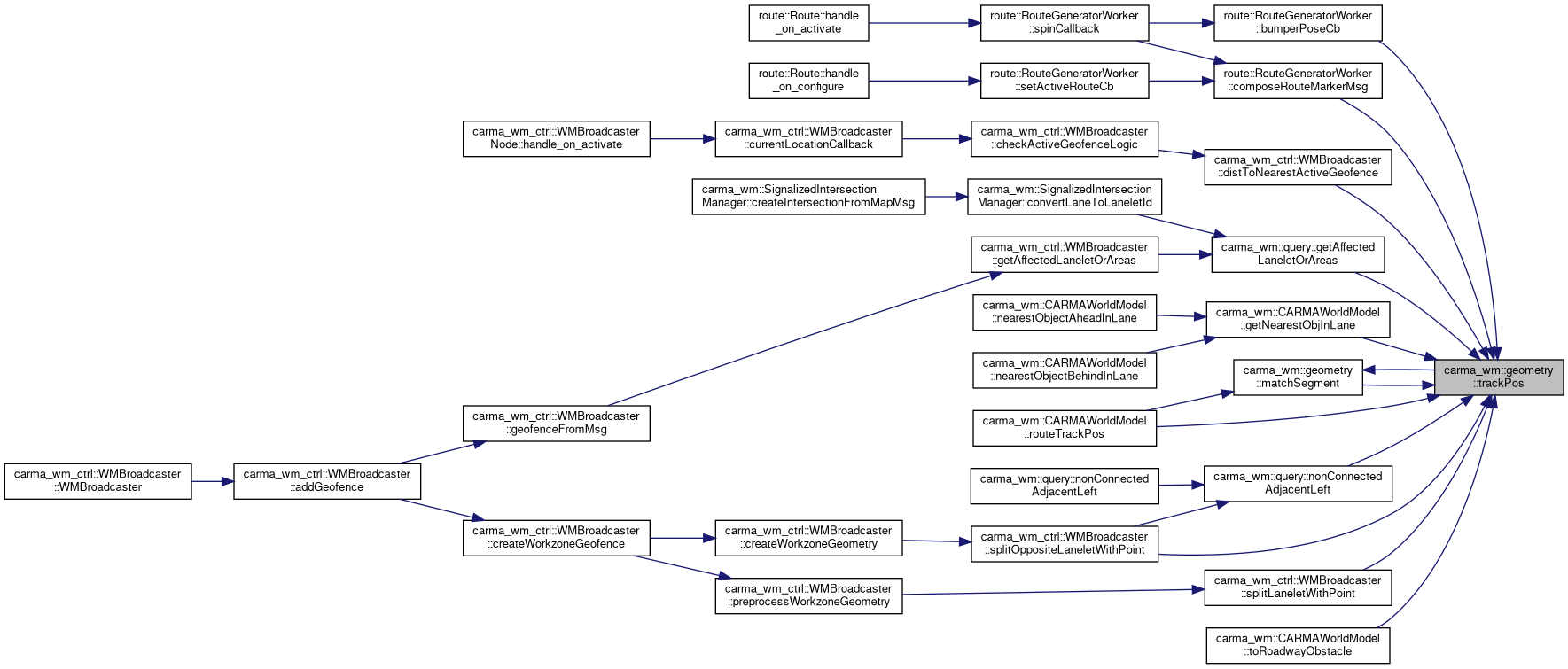
trackPos() [1/2]

TrackPos carma_wm::geometry::trackPos	(	const lanelet::BasicPoint2d &	p,
		const lanelet::BasicPoint2d &	seg_start,
		const lanelet::BasicPoint2d &	seg_end
	)

Return the track position of a point relative to a line segment defined by two other points. Positive crosstrack will be to the right. Points occuring before the segment will have negative downtrack.

Parameters

p	The point to find the TrackPos of
seg_start	The starting point of a line segment
seg_end	The ending point of a line segment

Returns

The TrackPos of point p relative to the line defined by seg_start and seg_end

Calculate the sign of the crosstrack distance by projecting the points to 2d d = (p_x - s_x)(e_y - s_y) - (p_y - s_y)(e_x - s_x) Equivalent to d = (start_to_p.x * start_to_end.y) - (start_to_p.y * start_to_end.x)

Code below based on math equation described at https://math.stackexchange.com/questions/274712/calculate-on-which-side-of-a-straight-line-is-a-given-point-located Question asked by user Ritvars (https://math.stackexchange.com/users/56723/ritvars) and answered by user Shard (https://math.stackexchange.com/users/55608/shard) Attribution here is in line with Stack Overflow's Attribution policy cc-by-sa found here: https://stackoverflow.blog/2009/06/25/attribution-required/

Calculate the sign of the crosstrack distance by projecting the points to 2d d = (p_x - s_x)(e_y - s_y) - (p_y - s_y)(e_x - s_x) Equivalent to d = (start_to_p.x * start_to_end.y) - (start_to_p.y * start_to_end.x)

Code below based on math equation described at https://math.stackexchange.com/questions/274712/calculate-on-which-side-of-a-straight-line-is-a-given-point-located Question asked by user Ritvars (https://math.stackexchange.com/users/56723/ritvars) and answered by user Shard (https://math.stackexchange.com/users/55608/shard) Attribution here is in line with Stack Overflow's Attribution policy cc-by-sa found here: https://stackoverflow.blog/2009/06/25/attribution-required/

Definition at line 76 of file Geometry.cpp.

{
  Eigen::Vector2d vec_to_p(p);
  Eigen::Vector2d vec_to_start(seg_start);
  Eigen::Vector2d vec_to_end(seg_end);
 
  // Get vector from start to external point
  Eigen::Vector2d start_to_p = vec_to_p - vec_to_start;
 
  // Get vector from start to end point
  Eigen::Vector2d start_to_end = vec_to_end - vec_to_start;
 
  // Get angle between both vectors
  double interior_angle = getAngleBetweenVectors(start_to_p, start_to_end);
 
  // Calculate downtrack distance
  double start_to_p_mag = start_to_p.norm();
  double downtrack_dist = start_to_p_mag * std::cos(interior_angle);
 
  double d = (start_to_p[0] * start_to_end[1]) - (start_to_p[1] * start_to_end[0]);
  double sign = d >= 0 ? 1.0 : -1.0;  // If d is positive then the point is to the right if it is negative the point is
                                      // to the left
 
  double crosstrack = start_to_p_mag * std::sin(interior_angle) * sign;
 
  return TrackPos(downtrack_dist, crosstrack);
}

References getAngleBetweenVectors().

Here is the call graph for this function:

trackPos() [2/2]

TrackPos carma_wm::geometry::trackPos	(	const lanelet::ConstLanelet &	lanelet,
		const lanelet::BasicPoint2d &	point
	)

Returns the TrackPos, computed in 2d, of the provided point relative to the centerline of the provided lanelet. Positive crosstrack will be to the right. Points occuring before the segment will have negative downtrack. See the matchSegment function for a description of the edge cases associated with the max_crosstrack parameter.

Parameters

lanelet	The lanelet whose centerline will serve as the TrackPos reference line
point	The lanelet2 point which will have its distance computed
max_crosstrack	The maximum crosstrack distance allowed for a perfect centerline segment match. See the matchSegment function for details

Exceptions

std::invalid_argument

If the lanelet centerline cannot be found

Returns

The TrackPos of the point relative to the lanelet centerline

Definition at line 120 of file Geometry.cpp.

{
  auto center_line = lanelet::utils::to2D(lanelet.centerline());
 
  if (center_line.numSegments() < 1)
  {
    throw std::invalid_argument("Provided lanelet has invalid centerline containing no points");
  }
  auto tuple = matchSegment(point, center_line.basicLineString());
 
  return std::get<0>(tuple);
}

References matchSegment(), and process_traj_logs::point.

Referenced by route::RouteGeneratorWorker::bumperPoseCb(), route::RouteGeneratorWorker::composeRouteMarkerMsg(), carma_wm_ctrl::WMBroadcaster::distToNearestActiveGeofence(), carma_wm::query::getAffectedLaneletOrAreas(), carma_wm::CARMAWorldModel::getNearestObjInLane(), matchSegment(), carma_wm::query::nonConnectedAdjacentLeft(), carma_wm::CARMAWorldModel::routeTrackPos(), carma_wm_ctrl::WMBroadcaster::splitLaneletWithPoint(), carma_wm_ctrl::WMBroadcaster::splitOppositeLaneletWithPoint(), and carma_wm::CARMAWorldModel::toRoadwayObstacle().

Here is the call graph for this function:

Here is the caller graph for this function:

Variable Documentation

SPATIAL_EPSILON_M

constexpr double carma_wm::geometry::SPATIAL_EPSILON_M = 0.05

constexpr

Definition at line 28 of file Geometry.cpp.

Referenced by concatenate_line_strings().